SEM via lavaan syntax in jamovi

keywords semlj,jamovi, lavaan, SEM

SEMLj lavaan syntax module of the SEMLj suite for jamovi

0.8.*

Draft version, mistakes may be around

Introduction

The SEMLj module is a jamovi interface to lavaan R package (Rosseel 2012). The module offers a syntax interface in which lavaan syntax for the model definition can be passed to the module. Almost everything you can pass in lavaan, you can pass it to SEMLj. All the available options are in the foldable panels below the syntax field. Thus, it is recommended that the user takes a look at lavaan website for details.

User Interface

When installed, the module sub-modules can be found in the SEM menu.

Here we need SEM (syntax).

Syntax field

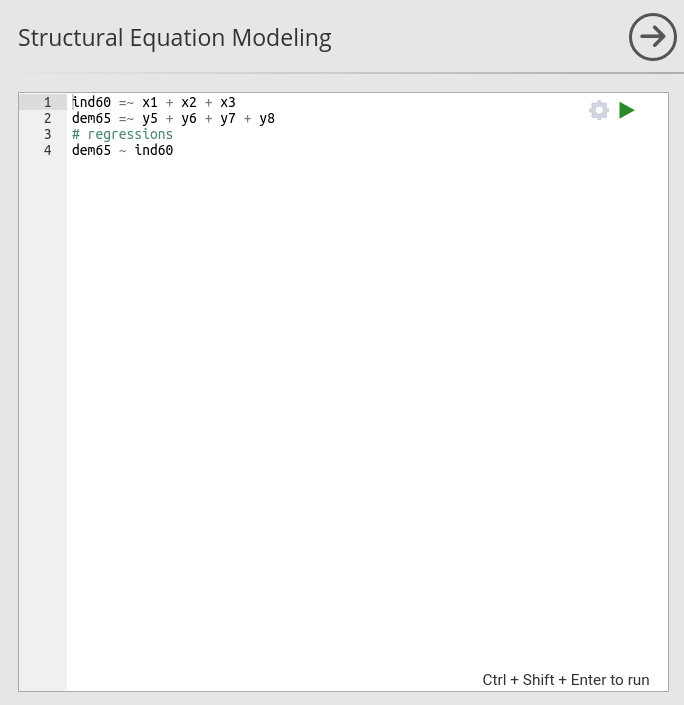
The syntax panel accepts lavaan syntax as described in lavaan website.

Note:

The syntax field accepts the lavaan syntax to define a model, not lavaan options or commands. For options, please use the options panels beneath the syntax field.

Warning:

Whereas any syntax you submit will be passed to lavaan::lavaan(), SEMLj may be not ready to understand the results and frame them in the output tables. At the moment, we have tested:

Path analysis models
Structural Equation models
Confirmatory Factor Analysis
Multigroup Analysis
Multilevel Models
Defined parameters (i.e a:=p1^2)
free and fixing parameters via model syntax (i.e x~~x or a~0*1)

Type of variables

To obtain a standard SEM model, please be sure that the observed variables are marked as continuous variable in the dataset. You see a little ruler icon on the left of the variable name, like this:

When variables are defined as continuous, they are considered continuous variables in SEMLj.

Categorical variables can be analyzed if they are defined as dichotomous or ordinal variable. SEMLj treats variables as ordered variables if they are defined as Nominal or Ordinal in the dataset, like this:

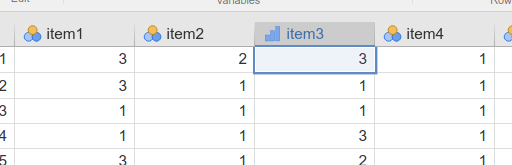
When indicators are ordinal or nominal, Diagonal Weighted Least Squares is used for estimation, with robust standard error. Please refer to lavaan documentation for more details.

Parameters labels

Any coefficient can be labeled in the syntax following lavaan syntax standard:

      x =~ a1*x1 + a2*x2 + a3*x3
      y =~ y1 + y2 +y3

This would attach the labels a1, a2 and a3 to the corresponding coefficient.

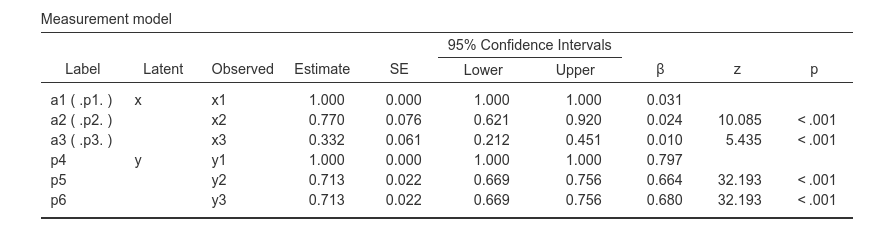
SEMLj automatically assigns a label to any coefficient, naming them pN, where N is an increasing integer. So, for y1, y2 and y3 in the example, a label of p4, p5 and p6 are assigned. User defined and automatically assigned labels can be used in the syntax in the same way. For instance:

      x =~ a1*x1 + a2*x2 + a3*x3
      y =~ y1 + y2 +y3  
      a1==p4
      a2==a3
      p5==p6

produced the desired constraints and relative tests.

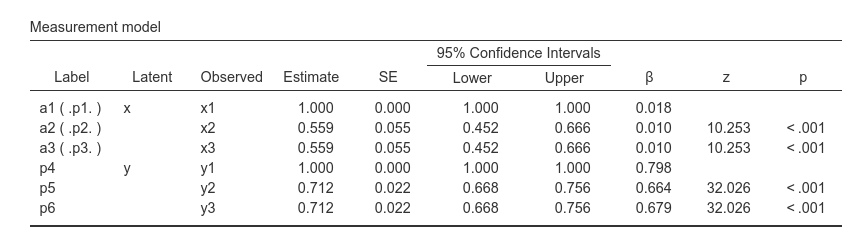
For used defined labels, the tables show also the internal automatic label uniquely assigned to the coefficients, with dots. a1 (.p1.) means the coefficient labelled by the user as a1 but internally referred to as .p1.. This additional information regarding the internal label is usefull in some cases of equality constraints.

Consider this syntax:

  y =~ y1 + a*y2 + a*y3 + a*y4

This asks for a latent variable scaled at y1, but with the loading of y2,y3 and y4 estimated as equal.

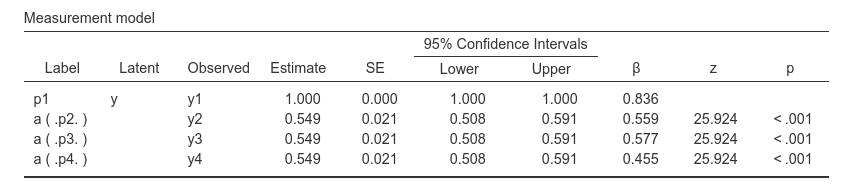
This also produces the tests for the pairwise comparisons of the coefficients.

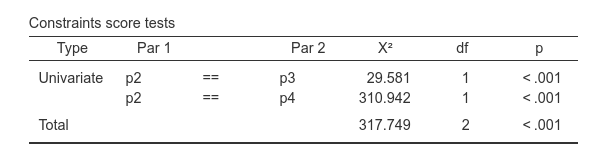
By comparing the uniquely assigned label (p2, p3, p4), we know which comparison is tested.

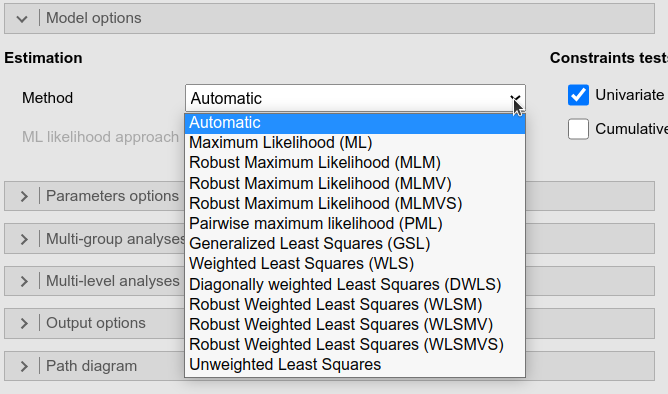
The Estimation Method allows choosing the right estimation method available for a model. The Automatic option (default) lets lavaan choose the right method depending to the type of model one is estimating.

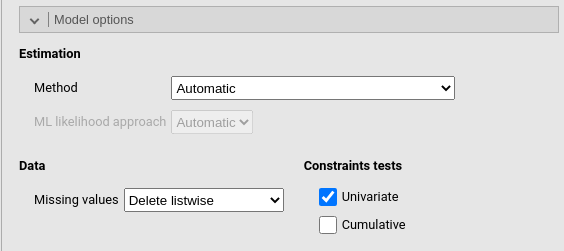
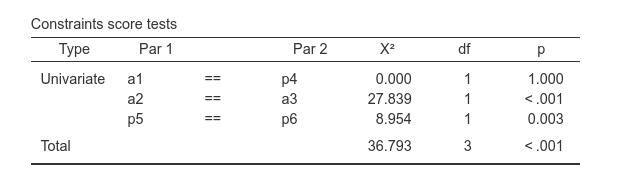
Constraints tests computes the \(\chi^2\) test for contrainted coefficients (if any). In case one has more than one contraints, each constraint is tested uniquely (if Univariate is flagged) and in addition to the previous ones (if Cumulative is flagged).

Under Data one can decide how to handle missing values.

The options for this panel are are:

Method	The estimator to be used (cf. lavaan R package). Can be one of the following: “ML” for maximum likelihood, “GLS” for (normal theory) generalized least squares, “WLS” for weighted least squares (sometimes called ADF estimation), “ULS” for unweighted least squares, “DWLS” for diagonally weighted least squares, and “DLS” for distributionally-weighted least squares. These are the main options that affect the estimation. For convenience, the “ML” option can be extended as “MLM”, “MLMV”, “MLMVS”, “MLF”, and “MLR”. The estimation will still be plain “ML”, but now with robust standard errors and a robust (scaled) test statistic. For “MLM”, “MLMV”, “MLMVS”, classic robust standard errors are used (se=“robust.sem”); for “MLF”, standard errors are based on first-order derivatives (information = “first.order”); for “MLR”, `Huber-White` robust standard errors are used (se=“robust.huber.white”). In addition, “MLM” will compute a Satorra-Bentler scaled (mean adjusted) test statistic (test=“satorra.bentler”), “MLMVS” will compute a mean and variance adjusted test statistic (Satterthwaite style) (test=“mean.var.adjusted”), “MLMV” will compute a mean and variance adjusted test statistic (scaled and shifted) (test=“scaled.shifted”), and “MLR” will compute a test statistic which is asymptotically equivalent to the Yuan-Bentler T2-star test statistic (test=“yuan.bentler.mplus”). Analogously, the estimators “WLSM” and “WLSMV” imply the “DWLS” estimator (not the “WLS” estimator) with robust standard errors and a mean or mean and variance adjusted test statistic. Estimators “ULSM” and “ULSMV” imply the “ULS” estimator with robust standard errors and a mean or mean and variance adjusted test statistic.
ML likelihood approach	Only relevant for ML estimation. If “Wishart”, the Wishart likelihood approach is used. In this approach, the covariance matrix has been divided by N-1, and both standard errors and test statistics are based on N-1. If “Normal” or “Automatic”, the normal likelihood approach is used. Here, the covariance matrix has been divided by N, and both standard errors and test statistics are based on N.
Missing values	Handling of missing values. `listwise` delete rows with missing. `FIML` for ‘full information’ maximum likelihood estimation. `FIML (including fixed x)` for ‘full information’ maximum likelihood estimation that includes also the fixed exogenous variables. `Two stages (robust)` uses a two stage appraoch whereas `Pairwise` deletes case pairwise before computing the covariances between variables.
Univariate	Score test (or Lagrange Multiplier test) for fixed or constrained parameters in model.
Cumulative	Score test for all fixed or constrained parameters in model (cumulative tests).

Type of models

Users familiar with lavaan or with lavaan documentations may want to distinguish between different types of models, namely, cfa (confirmatory factor analysis), sem (structural equation models) and growth (individual growth models). These models enjoy the same underlying estimation procedure, but they are different in the options passed to lavaan. In SEMLj, one can obtain the same results as sem and cfa setup using the default options settings (unless you know you need some change). For growth model type, one needs to set Intercepts->Observed variables to false (unselect it), and Intercepts->Latent variables to true (select it) in the Parameters Options panel, and you’re a happy camper.

Model parameters

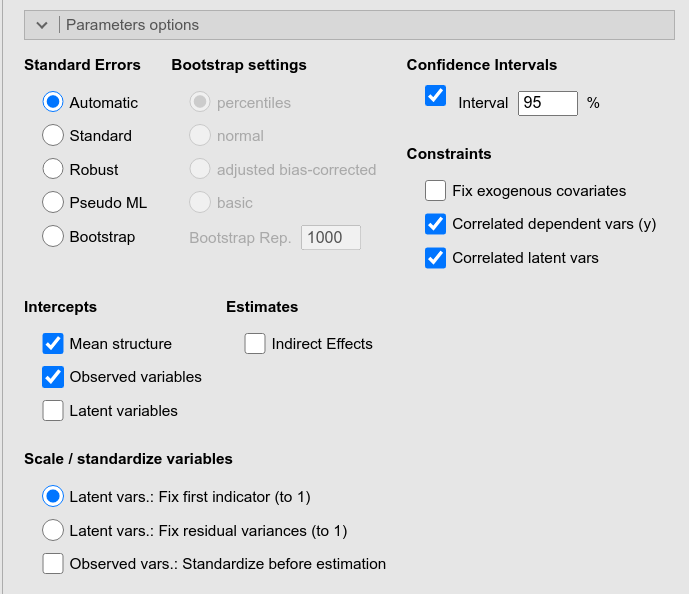
This panel offers many options to be passed to lavaan for specify parameters charateristics, such as how to compute their standard errors, their confidence intervals, or how to fix scales of latent variables.

In addition, it offers the Indirect Effects option which computes and estimate all possible indirect effects (from exogenous to endogenous variables) present in the model.

The options are:

Standard errors	Standard error method.
Bootstrap C.I	Choose the confidence interval type (“perc” - percentiles [default], “bca.simple” - adjusted bias-corrected, “norm” - normal, “basic” - basic).
Bootstrap Rep.	The number of bootstrap samples for estimating confidence intervals.
Parallel Computation	use parallel computation for bootstrap C.I
Estimates	`TRUE` or `FALSE` (default), show confidence intervals for estimates
Betas	`TRUE` or `FALSE` (default), show confidence intervals for standardized estimates
Confidence level	A number between 50 and 99.9 (default: 95) specifying the confidence interval width for the parameter estimates.
Fix exogenous covariates	If `TRUE`, the exogenous covariates are considered fixed variables and the means, variances and covariances of these variables are fixed to their sample values. If `FALSE`, they are considered random, and the means, variances and covariances are free parameters. If “default”, the value is set depending on the mimic option.
Mean structure	If TRUE, the means of the observed variables enter the model. Required for calculating the intercepts of the estimates.
Observed variables	`TRUE` or `FALSE` (default), calculate intercepts for observed variables
Latent variables	`TRUE` or `FALSE` (default), calculate intercepts for latent variables
Indirect Effects	compute the indirect effect by finding all paths from exogenous to endogenous variables, and multiply the coefficients along the path.
Scale / stand. latent vars.	If `Fix first indicator` (default), the factor loading of the first indicator is set to 1.0 for every latent variable. If `Fix residual variances`, the metric of each latent variable is determined by fixing their (residual) variances to 1.0. If there are multiple groups, `Fix residual variances` is chosen and “loadings” is included in the group.label argument, then only the latent variances i of the first group will be fixed to 1.0, while the latent variances of other groups are set free.
Observed vars.: Standardize before estimation	If set, all observed variables are standardized before entering the analysis.

Multi-group Analysis

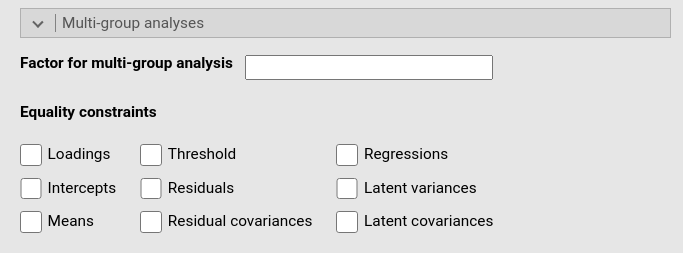
This panel allows for specifying a categorical variable (factor) defining groups of multi-group analysis. One simply writes the name of the factor variable in the Factor for multi-group analysis field.

Once a multi-group analysis is set, one can choose which parameter to fix as equal across groups.

The options are:

Loadings	constrain the factor loadings to be equal across groups (when conducting multi-group analyses)
Intercepts	constrain the intercepts of the observed variables to be equal across groups (when conducting multi-group analyses)
Means	constrain the intercepts / means of the latent variables to be equal across groups (when conducting multi-group analyses)
Threshold	constrain the sample-based thresholds (means for continuous observed mvariables) to be equal across groups (when conducting multi-group analyses)
Residuals	constrain the residual variances of the observed variables to be equal across groups (when conducting multi-group analyses)
Residual covariances	constrain the residual covariances of the observed variables to be equal across groups (when conducting multi-group analyses)
Regressions	constrain all regression coefficients in the model to be equal across groups (when conducting multi-group analyses)
Latent variances	constrain the (residual) variances of the latent variables to be equal across groups (when conducting multi-group analyses)
Latent covariances	constrain the (residual) covariances of the latent variables to be equal across groups (when conducting multi-group analyses)

Multilevel Analysis

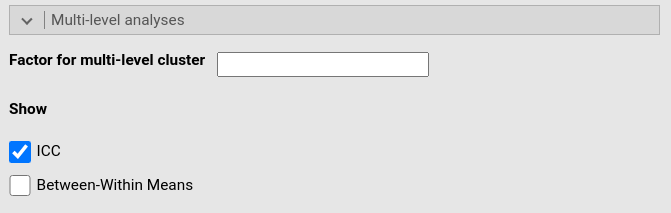
This panel allows specifying a categorical variable (factor) defining cluster variable of multgroup analysis. One simply writes the name of the factor variable in the Factor for multi-group analysis field.

Once a cluster is set, the right syntax for specifying the multilevel model should be set in the syntax panel. See deailts here.

Output Options

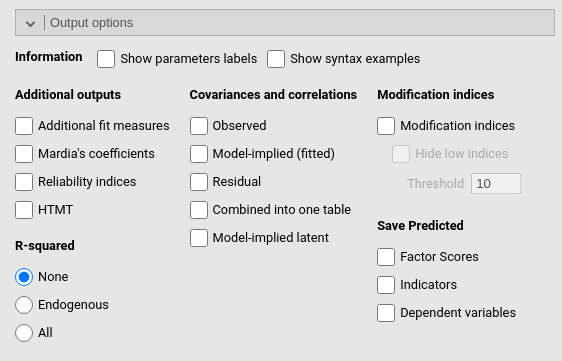
This panel allows requesting all sort of additional information about the model results, such as the \(R^2\)’s, the implied and residual variances and covariances, and the modification indexes.

It is worth mentioning the option to save the predicted and residuals in the dataset. The Predicted option saves, for each participant, the model based predicted values of the observed variables involved in the measurement of purely endogenous dependent variables. The predicted values computation is based on Rooij et al. (2022), and the implementation is adpted from github SEMpredict

The other options are:

Show parameters labels	show the labels of the parameters in the model
Show syntax examples	show examples of the lavaan model syntax
Show Lavaan Options	show options of the lavaan model
Additional fit measures	show additional fit measures (e.g., CFI, TLI, etc.)
Mardia’s coefficients	show Mardia’s coefficients for multivariate skewness and kurtosis
Reliability indices	shows additional reliability indices
HTMT	`TRUE` or `FALSE` (default), show Heterotrait-monotrait (HTMT) ratio of correlations as reccomended by Henseler, Ringle, and Sarstedt (2015)
R-squared	compute R-squared for all endogenous variables (`Endogenous`) or for all variables in the model (`All`). `None` for no R-squared.
Observed	show the covariances and correlations between the observed values of the (manifest) variables
Model-implied (fitted)	show the covariances and correlations between the model-implied / fitted values of the (manifest) variables
Residual	show the covariances and correlations between the residuals of the (manifest) variables.
Combined into one table	combine the (up to) three covariance / correlation tables into one table (i.e., showing observed, model-implied and residual values for each variable combination underneath each other)
Model-implied latent	show model-implied latent covariances
Modification indices	show modification indices for if certain terms were removed from the model
Hide low indices	hide modification indices below a certain threshold.
Threshold	Numeric (default: 10), set a threshold the modification indices must exceed in order to be shown.
Factor Scores	this option saves, for each participant, the latent variables predicted values based on the latent variables estimation. The values are obtained with `lavaan::lavPredict(..,type="lv")`. See Rosseel (2012) for details. The values are basically factor scores.
Indicators	this option saves, for each participant, the observed variables predicted values based on the latent variables estimation. The values are obtained with `lavaan::lavPredict(..,type="ov")`. See Rosseel (2012) for details
Dependent variables	this option saves, for each participant, the model based predicted values of the observed variables involved in the measurement of purely endogenous dependent variables. The predicted values computation is based on Rooij et al. (2022), and the implementation is adpted from github SEMpredict

The name of the new variables saved in the datasheet are indicated in a footnote of the Info Table.

Path Diagram

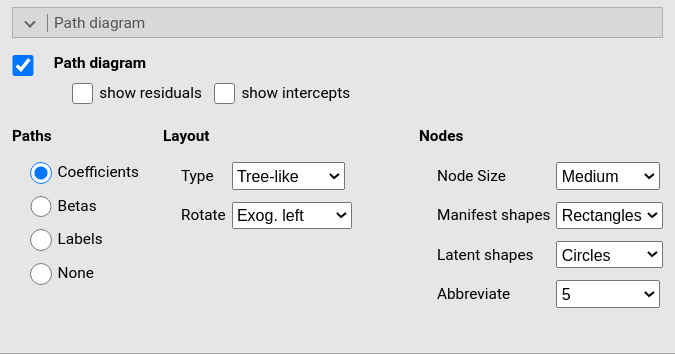
This panel produces the path diagram graph and allow for some change in shapes and orientation of the diagram. The digram is produced using R semPlot module, see also (Epskamp 2015)

The options are:

Path diagram	produce a path diagram.
show residuals	show the residuals (for the observed variables).
show intercepts	show the variable intercepts.
Paths Labels	Choose the values shown along the paths.
Type	Choose the layout of the path diagram: `Tree`, `Tree2`,`Circle`,`Circle2` , `Spring`).
Rotate	Choose the rotation of the path diagram in terms of placement of the exog. variables.
Node Size	Choose the node size for the variables (default: “medium”).
Manifest shapes	Choose the shape for the manifest variables (default: “rectangle”).
Latent shapes	Choose the shape for the latent variables (default: “circle”).
Abbreviate	Choose the length (characters) of the variable name abbreviations (default: 5).

Examples

Some worked out practical examples can be found here

Details

Some more information about the module specs can be found here

SEMLj computation details

Comments?

Got comments, issues or spotted a bug? Please open an issue on SEMLj at github or send me an email

References

Epskamp, Sacha. 2015. “semPlot: Unified Visualizations of Structural Equation Models.” Structural Equation Modeling: A Multidisciplinary Journal 22 (3): 474–83.

Henseler, Jörg, Christian M Ringle, and Marko Sarstedt. 2015. “A New Criterion for Assessing Discriminant Validity in Variance-Based Structural Equation Modeling.” Journal of the Academy of Marketing Science 43: 115–35.

Rooij, Mark de, Julian D. Karch, Marjolein Fokkema, Zsuzsa Bakk, Bunga Citra Pratiwi, and Henk Kelderman. 2022. “SEM-Based Out-of-Sample Predictions.” Structural Equation Modeling: A Multidisciplinary Journal 0 (0): 1–17. https://doi.org/10.1080/10705511.2022.2061494.

Rosseel, Yves. 2012. “lavaan: An R Package for Structural Equation Modeling.” Journal of Statistical Software 48 (2): 1–36. https://www.jstatsoft.org/v48/i02/.