The data

For this example we are going to use the Demo.twolevel dataset present in lavaan R package, which is useful for estimating a multilevel model, with a small modification. The dataset contains 200 clusters, within each 6 items (y1-y2) and 3 continuous variables (x1-x3) are measured. Across clusters (between level) two covariates (w1 and w2) are measured .

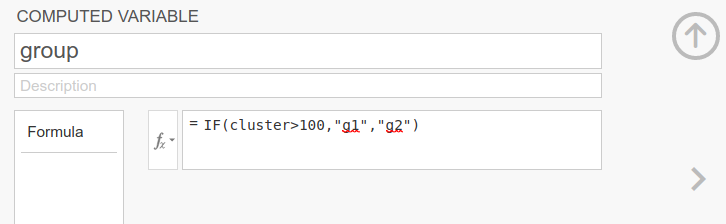
We now imagine that the 200 clusters are evenly divided in two groups, g1 and g2. Had this dataset been based on a survey in 200 school classes, for instance, one can imagine that 100 classes came from one state (g1) and the other 100 from another state. We created the group variable on the spot for the sake of this exercise.

We want to estimate the multilevel model (cf lavaan help page), in the whole sample, then separated for the two groups, and test some differences in parameters between the two groups.

The model (whole sample)

The model has a latent variable measured within clusters (fw) with 3 items y1,y2,y3. At the within-cluster level, the latent variable is predicted by the three covariates x1, x2 and x3.

At the between-cluster level, the same latent variable is present measured with the same items (fb=y1+y2+y3), but it is predicted by the two between-cluster covariates (w1 and w2). Here is the model for the whole sample.

    level: within
        fw =~ y1 + y2 + y3
        fw ~ x1 + x2 + x3
    level: between
        fb =~ y1 + y2 + y3
        fb ~ w1 + w2

Output

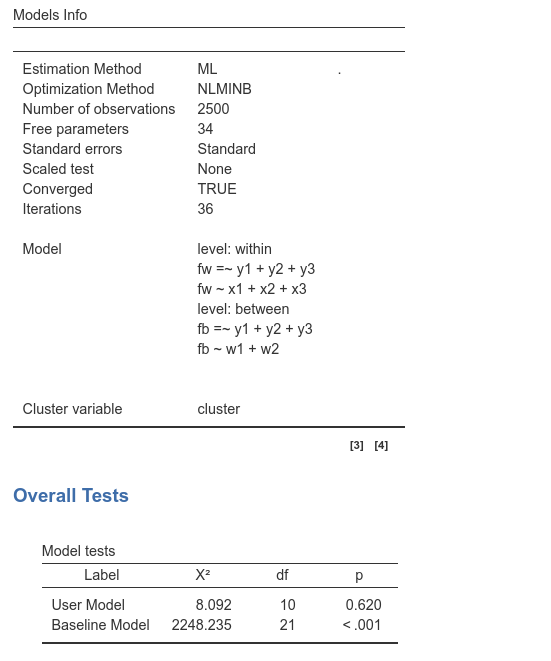
As soon as we set the input, we obtain the whole set of results tables. We do not go through the results now, because this is not the model we are focusing on, but we need to be sure that the estimation converges in the whole sample, so we are ready for the multigroup analysis. In fact, if the model does not converge in the whole sample, it is difficult to make it converge in multigroup analysis.

Multigroup model

We now set the multigroup analysis on top of the multilevel model. The model syntax needs to be repeated for the two groups explicitly. Important point: whereas standard multigroup analysis only requires to define a grouping variable in the Multi-group analysis panel, here we need to specify a grouping variable in the Multigroup analysis panel and the grouping structure in the syntax.

There you go: First, we set the multigroup variable

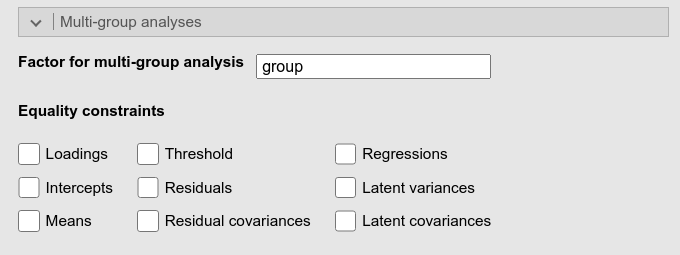
and then we issue the following syntax:

group: g1
    level: within
        fw =~ y1 + y2 + y3
        fw ~ x1 + x2 + x3
    level: between
        fb =~ y1 + y2 + y3
        fb ~ w1 + w2
group: g2
    level: within
        fw =~ y1 + y2 + y3
        fw ~ x1 + x2 + x3
    level: between
        fb =~ y1 + y2 + y3
        fb ~ w1 + w2

At this point, we have all our estimated parameters, for the within and the between level, divided by group.

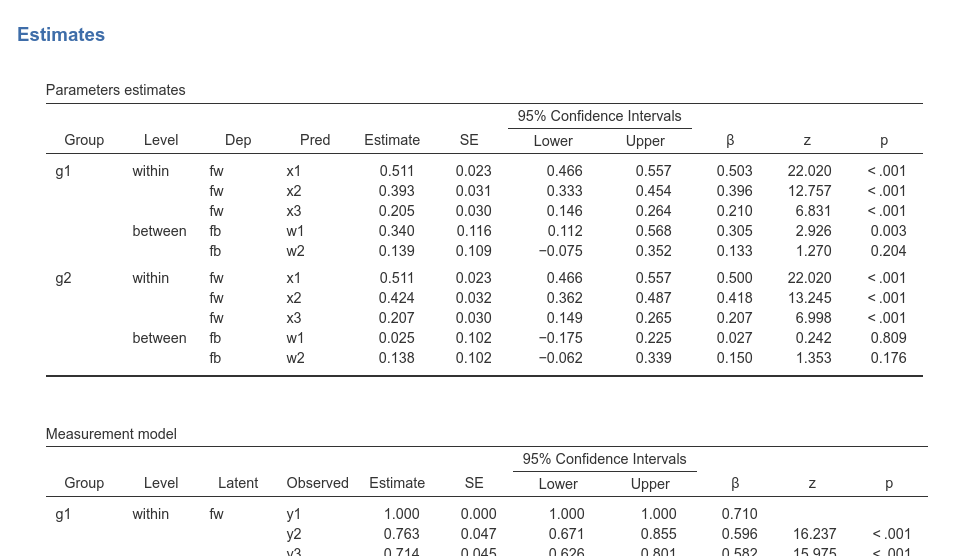
If the model works, we can start testing equality constraints across groups. However, for this particular model, the Equality constraints options in the input panel cannot be used to quickly set the constraints. We need to use the syntax. But before, let’s ask for the parameter labels, so we can identify parameters in the output.

Constraints across groups

Assume we want to test that measurement model at the within level is the same across groups. So we want to test that fw =~ y1 + y2 + y3 is equivalent across groups. We need to set this syntax (notice the labels a2 and a3):

group: g1
    level: within
        fw =~ y1 + a2*y2 + a3*y3
        fw ~ x1 + x2 + x3
    level: between
        fb =~ y1 + y2 + y3
        fb ~ w1 + w2
group: g2
    level: within
        fw =~ y1 + a2*y2 + a3*y3
        fw ~ x1 + x2 + x3
    level: between
        fb =~ y1 + y2 + y3
        fb ~ w1 + w2

By setting the same coefficients across groups (a2,a3), we set the parameters as constrained to be equal across groups. We do not need to fix y1 because it is already fixed to 1 to give the latent variable a scale.

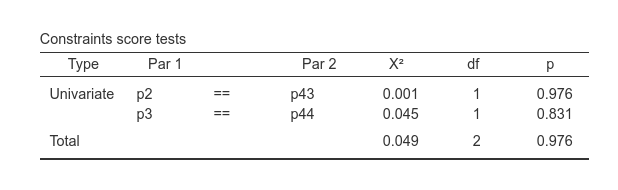
Passing this syntax produces in the output the tests for these constraints.

To clearly understand what is going on, please check the parameter labels in the tables.

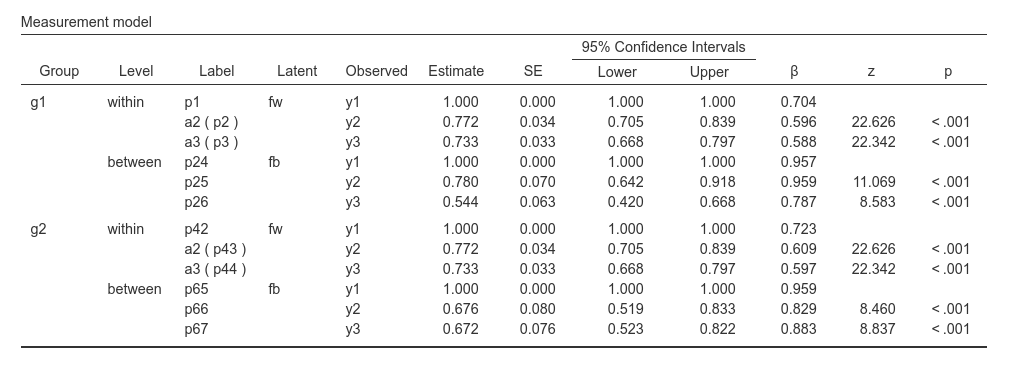
The loading fw->y2 has a label a2 (p2) for group 1 and a2 (p43) for group 2. This means that the user declared the label a1 for both, and each is uniquely referred to as p2 for group 1 and p43 for group 2. The same goes for a3.

Now, in the constraints tests table, we see the test for the equality of a2, because the test is comparing p2 vs p43, and for a3, because the test is comparing p3 with p44. We also get the overall test Total.

With this method, we can test any constraint we wish.

Related examples